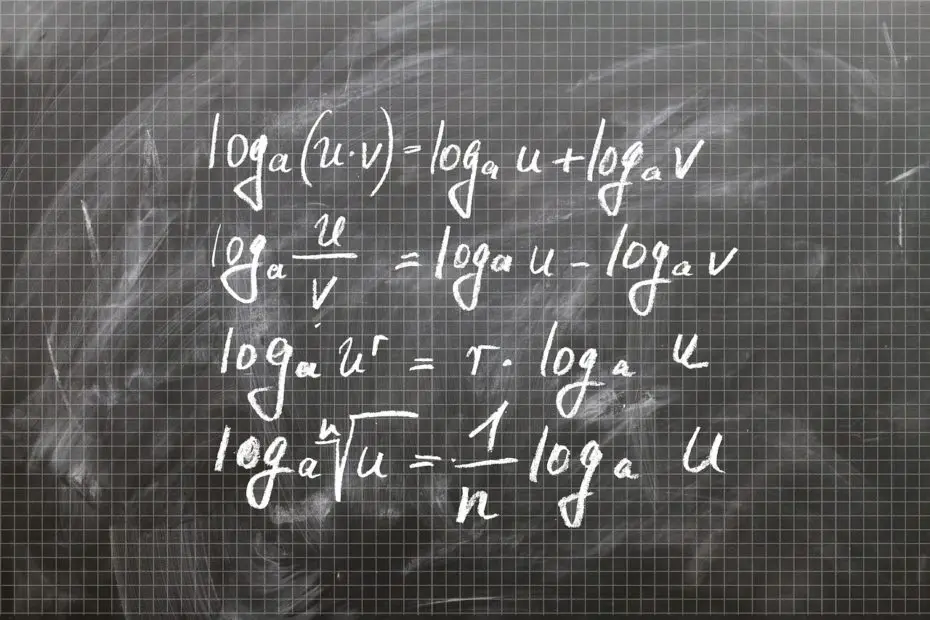Cuando hablamos de logaritmo, nos referimos a un exponente que se necesita elevar utilizando una cantidad determinada para obtener un número positivo o negativo dependiendo el caso. En resumen, es el exponente de una potencia que cuenta con cierta base, es decir que allí se indica el número por el cuál debe elevarse como ocurre, por ejemplo, cuando realizamos una operación como 3²=9 o 2²=4.
A continuación, te contaremos todo lo que debes saber sobre los logaritmos y cuáles son sus principales propiedades, ¡sigue leyendo!
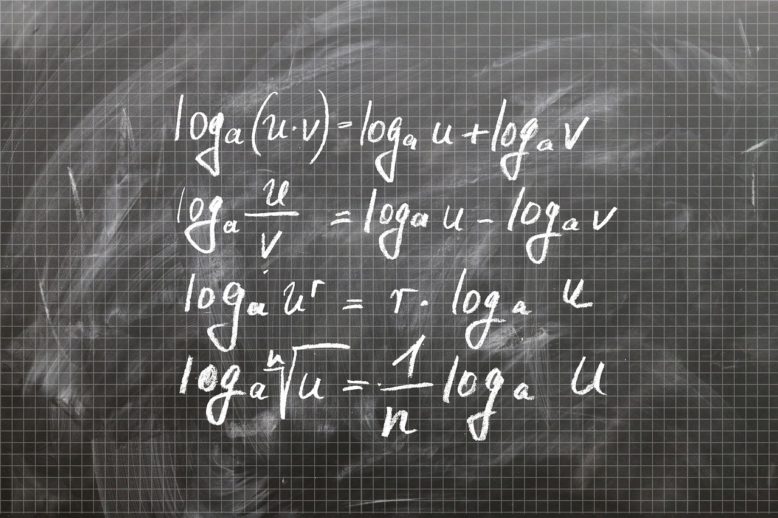
Temas del artículo
¿Cuál es el uso de los logaritmos?
Desde su descubrimiento, los logaritmos se han convertido en una poderosa herramienta que permite realizar operaciones con cifras de gran tamaño y que cuentan con exponentes altos. Tiene la capacidad de simplificar operaciones que, si se realizan de otra manera, pueden ser muy complicadas.
Tipos de logaritmos
Existen dos tipos de logaritmos que se utilizan comúnmente en operaciones matemáticas.
Logaritmos naturales o neperianos: son los logaritmos que tienen como base el número “e” el cual consiste en una constante que es igual a 2.718. Estos se utilizan en cálculos estadísticos y para obtener cifras de los distintos fenómenos naturales como ocurre con la descomposición por radioactividad.
Logaritmos comunes: son aquellos que tienen como base el número 10. Se emplean para medir el pH de cualquier líquido y para otros fenómenos químicos.
Propiedades de los logaritmos
Logaritmo del producto: Cuando existe un producto de factores, se suman dichos logaritmos.
log (a*b)= log(a) * log(b)
Logaritmo de un cociente: Cuando hay un cociente dentro de un logaritmo, se deben restar el numerador y el denominador.
log(a/b) = log(a)−log(b)
Logaritmo de una potencia: Cuando existe el logaritmo de una potencia, se debe multiplicar el exponente por el resultado del logaritmo en base de 10.
log(ab) = b*log(a)
Cambio de base: Si bien no se trata de una propiedad en si misma, es algo muy útil.
logb(a) = logc(a)
logc(b)
Es importante tener en cuenta que, para aplicar cualquiera de estas propiedades, los logaritmos deben tener siempre la misma base.
Etimología de la palabra logaritmo
La palabra logaritmo proviene del griego antiguo y se escribe como λόγος, que significa “razón” y ἀριθμός que quiere decir “número”.
Uso de los logaritmos en distintas disciplinas
- En la astronomía: La magnitud aparente que posee un objeto, si estuviera a una distancia de un año luz, podría obtenerse con una fórmula como: M=m + 5.log (d). En este caso, “d” equivale a la distancia en parsecs.
- En química: los logaritmos se utilizan para obtener el nivel de acidez de una fórmula (pH) e indica cuál es la concentración de iones. La fórmula utilizada es pH= -log(H*)
- En la arqueología: En esta ciencia, los investigadores utilizaban los logaritmos para saber cuál era la antigüedad de los restos orgánicos utilizando el método llamado “Carbono 14”. La fórmula es
t=T1/2 * ln(Nf)
-ln2 (No)
“No” es la cantidad de Carbono 14 que origina un fósil al morir y “Nf” es la cantidad de Carbono 14 al final de la ecuación. - En la música: Los logaritmos se emplean para saber cuál es el tipo de tonalidad de acuerdo al número de vibraciones y la longitud de onda. Se representan con los logaritmos en base 2 de dichas magnitudes. Esto se puede calcular con la siguiente fórmula: log2 N pm=m+p.
Los pentagramas, gracias a esta fórmula, tienen relación directa con los logaritmos. - En geología: se emplean para medir los movimientos de los sismos en la escala de Ritcher y también para medir la energía que se libera al momento de la rotura de las rocas. Las fórmulas que se utilizan son las siguientes: Para la energía liberada: logE=1.5*M-1,74. Para calcular los grados de la escala de Ritcher: R=log(A/b)
- En estadística: los logaritmos se usan para calcular la densidad y el crecimiento de la población de un territorio: log Pf = log Pa + n log(1+r). Pf corresponde a la cantidad de población futura.
Ejemplos de ejercicios resueltos con logaritmos
log2(8)=3
2³=8
log91/3 = X
9x = 1/3
(3²)x = 3-1
2X=-1
X=-1/2
log1/20,25 = X
(1/2)x=0,25
(1/2)x=1/4
2X = 4
X = 2
log 0,001 = X
10x = 0,001
10x = 1/1000
10x = 10-3
X = -3
log3(108) – 2log3(2) + log5(12,5) + log5(10)
log3(108) – 2log3(22) + log5(12,5) + log5(10)
log3(108) – 2log3(4) + log5(12,5) + log5(10)
log3(108/4) + log5(12,5 * 10)
log3(27) + log5(125)
log3(33) + log5(53)
3log3(3) + 3log5(5)
3+3
6
Preguntas frecuentes (FAQs)
Un logaritmo es el exponente que se necesita para elaborar una cantidad determinada y cuyo resultado es un número natural que puede ser positivo o negativo.
Además de utilizarse en la ciencias matemáticas, también se emplean en otras disciplinas como la química, para medir el pH de los líquidos, en geología con el fin de calcular la intensidad de los terremotos y en astronomía, entre otras ciencias.
Un logaritmo tiene como resultado 1 cuando la potencia es la misma que el número por el cuál se está realizando la ecuación.
Producto: se deben sumar los logaritmos de los factores.
División: se deben restar dichos factores.
Potencia: se debe multiplicar el producto del exponente por el logaritmo de la base.