La proposición 47 de Euclides que indica que BC² = BA² + AC², es un problema que tiene varios siglos. A grandes rasgos, gracias a esta proposición se descubrió que en un triángulo rectángulo, es decir aquel que cuenta con un ángulo recto de 90º, el lado opuesto a ese ángulo será igual a la suma de los dos lados restantes del triángulo elevados al cuadrado.
Esta proposición es aún utilizada en ciertos lugares como la construcción de viviendas, pues los albañiles y arquitectos se valen de ella para hacer mediciones con la escuadra al colocar ladrillos u otros elementos similares.
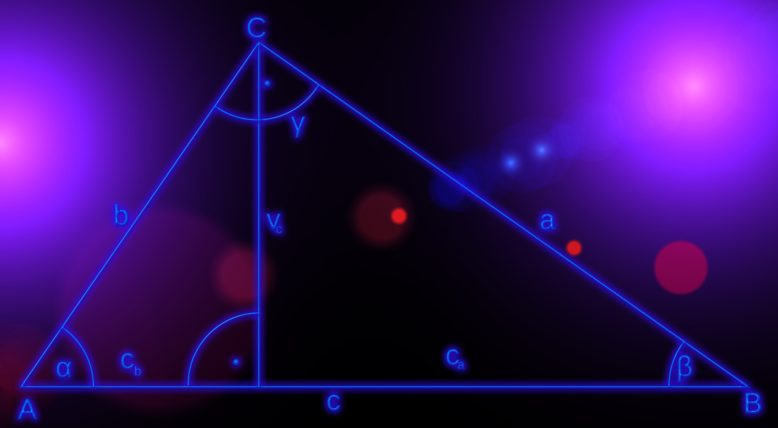
Explicación de la proposición 47 de Euclides
Para explicar la proposición 47 de Euclides debemos nombrar los ángulos interiores del triángulo con las letras A, B y C y el ángulo recto se encuentra en B, se puede decir que ΒC2=ΒΑ2+ΑC2. El primer paso es trazar un cuadrado desde el lado BC que se debe nombrar como BDEC. Posteriormente, se debe trazar otro que parta del lado BA que se deberá llamar GB y otro desde AC al que nombraremos como HC. Posteriormente, desde el punto A se deberá trazar una línea a la que llamaremos AL que deberá ser paralela a la recta BD o a la que llamamos CE.
A continuación se deberá trazar la línea AD y la FC. Como consecuencia, obtendremos otro ángulo recto en el triángulo formado por BAG. Esto significa que en cualquier recta BA y por un punto de ella, las dos rectas, llamadas AC y AG harán que sus ángulos adyacentes sean de 90º, es decir, rectos.
La recta CA se conecta con AG y lo mismo ocurre con AH. De allí, podemos inferir que el ángulo formado por DBC es igual al que se forma con las rectas FBC. Además sabemos que FΒ es igual a ΒΑ y que DΒ es lo mismo que ΒC. Esto significa que los dos lados DΒ y ΒΑ son iguales a FB y BC. Por otro lado el ángulo formado por DBA y el que se forma por FBC son similares. Esto quiere decir que la recta AD es igual ala recta FC. Por lo tanto el triángulo formado por ABD y el que forman FBC son exactamente iguales.
Además, el cuadrado formado por BDEC que fue trazado desde la recta BC y los cuadrados HC y GB que fueron dibujados desde AC y BA tienen también las mismas medidas. Es por esto mismo que se llega a la conclusión de que BC² = BA² + AC².
Teorema de Pitágoras
La proposición 47 de Euclides también se asemeja al teorema de Pitágoras. La diferencia es que este último se refiere a los lados de un triángulo. Por otro lado, el problema 47 hace alusión a los lados opuestos de los ángulos del triángulo rectángulo. El teorema de Pitágoras fue y es utilizado en muchos problemas de trigonometría. El fin es el de obtener las medidas de los lados de un triángulo rectángulo con una o dos medidas. Indica que el cuadrado de la hipotenusa (es decir el lado más largo de la figura) es igual a la suma de los cuadrados de los catetos, tanto el opuesto como también el adyacente. Hipotenusa²=Cateto opuesto² + Cateto adyacente² (a²=b² + c²).
